

But if your function is continuous at that x value, you will get a value, and youre done.
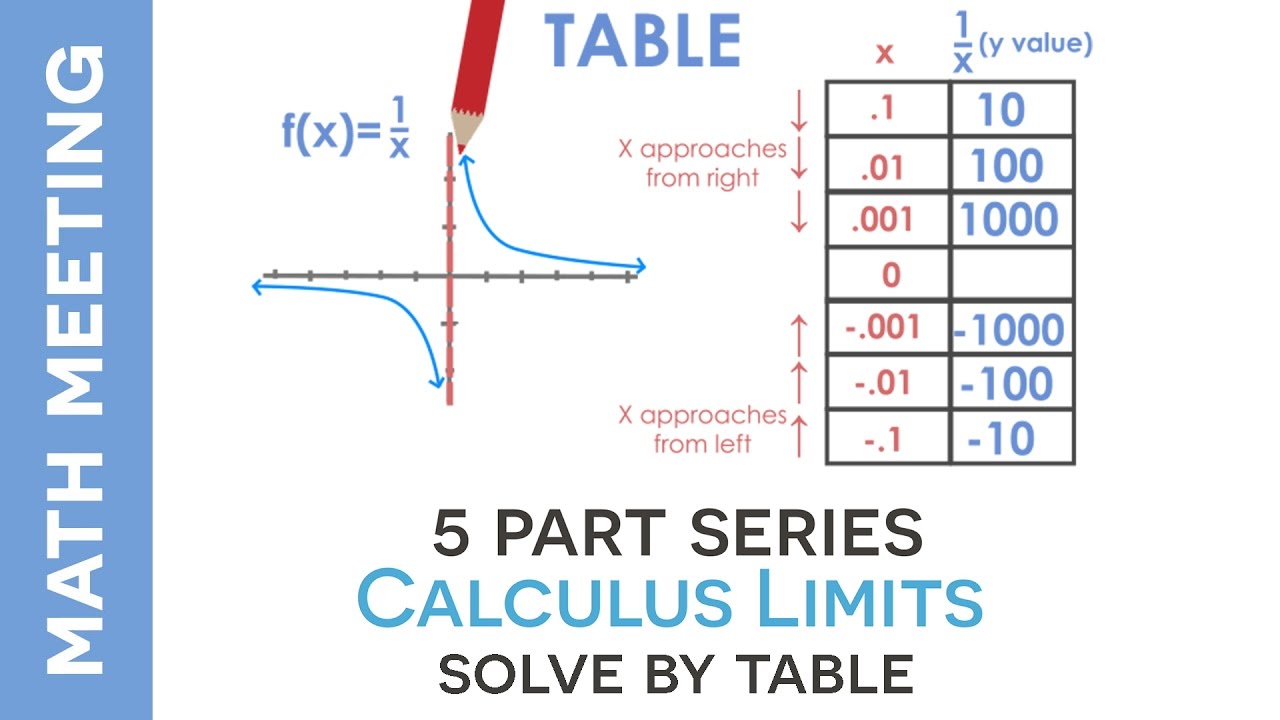
If you get an undefined value (0 in the denominator), you must move on to another technique. The first technique for algebraically solving for a limit is to plug the number that x is approaching into the function. For higher-order derivatives, certain rules, like the general Leibniz product rule, can speed up calculations.Lim x → c f ( x ) = L \lim_ = 1 lim x → 0 x s i n ( x ) = 1. Find the limit by plugging in the x value. Additionally, D uses lesser-known rules to calculate the derivative of a wide array of special functions. It uses well-known rules such as the linearity of the derivative, product rule, power rule, chain rule and so on. By the end of this lecture, you should be able to use the graph of a function to find limits for a number of different functions, including limits at infinity. Wolfram|Alpha calls Wolfram Languages's D function, which uses a table of identities much larger than one would find in a standard calculus textbook. A one sided limit is the value a function approaches as the x-value(s) approach the limit from one side only. For example, it is used to find local/global extrema, find inflection points, solve optimization problems and describe the motion of objects. Approaching the limit of x 3 from the right. Before proceeding with examples let me address the spelling of L’Hospital. The derivative is a powerful tool with many applications. So, L’Hospital’s Rule tells us that if we have an indeterminate form 0/0 or / / all we need to do is differentiate the numerator and differentiate the denominator and then take the limit.

Īs an example, if, then and then we can compute. Geometrically speaking, is the slope of the tangent line of at. This limit is not guaranteed to exist, but if it does, is said to be differentiable at. It is a mathematical way of saying 'we are not talking about when x, but we know as x gets bigger, the answer gets closer and closer to 0'. When you see 'limit', think 'approaching'. In other words: As x approaches infinity, then 1 x approaches 0. Note for second-order derivatives, the notation is often used.Īt a point, the derivative is defined to be. The limit of 1 x as x approaches Infinity is 0. These are called higher-order derivatives. When a derivative is taken times, the notation or is used. Given a function, there are many ways to denote the derivative of with respect to. What are derivatives? The derivative is an important tool in calculus that represents an infinitesimal change in a function with respect to one of its variables. Partial Fraction Decomposition Calculator.
#3 ways to find limits in calculus generator#
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
#3 ways to find limits in calculus how to#
Here are some examples illustrating how to ask for a derivative.
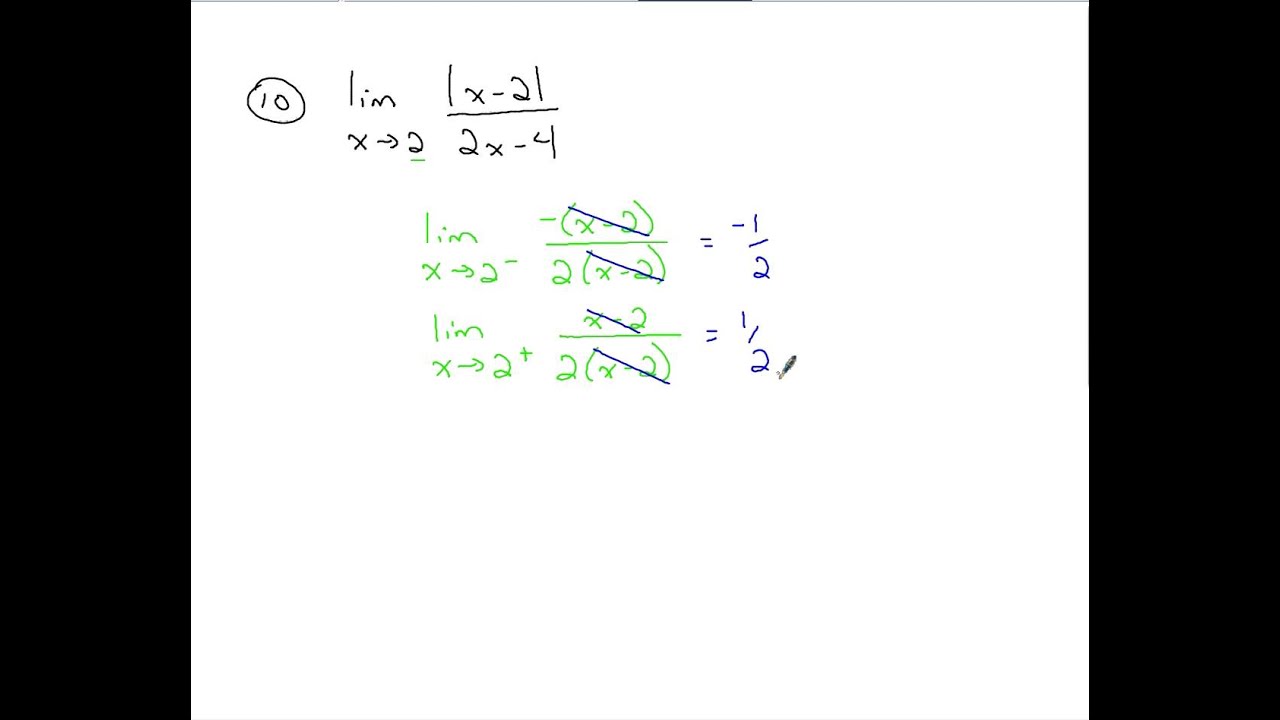
To avoid ambiguous queries, make sure to use parentheses where necessary. This fact can be turned around to also say that if the two one-sided limits have different values, i.e., lim xa+f (x) lim xaf (x) lim x a + f ( x) lim x a f ( x) then the normal limit will not exist. Learn what derivatives are and how Wolfram|Alpha calculates them.Įnter your queries using plain English. Overview and Indeterminate Forms and Rules 2 Examples of finding a limit using factoring 2 Examples of finding a limit using common denominators 2 Examples. A similar pseudo-definition holds for functions of two variables. Wolfram|Alpha is a great calculator for first, second and third derivatives derivatives at a point and partial derivatives. Recall a pseudo-definition of the limit of a function of one variable: ' lim x c f(x) L '' means that if x is 'really close'' to c, then f(x) is 'really close'' to L. More than just an online derivative solver If the position graphs are not piecewise linear, it is more difficult to find the slope at a given point on the graph.


 0 kommentar(er)
0 kommentar(er)
